Thomas Carey
Voxel Octree Engine
Site URL:
https://418-project.s3.amazonaws.com/index.html
Project Github: https://github.com/tmcarey/418Project
We built a ray-traced voxel render engine which uses an octree acceleration data structure and the tools we have learned in this class to efficiently render a game world which can be dynamically lit and manipulated. It uses a much higher voxel spatial resolution than most voxel game worlds, because the data structure we used not only effectively compresses the spatial information but also allows rendering high detail scenes extremely efficiently. We also wrote an algorithm which takes a gray-scale heightmap image - where the intensity at each pixel represents the elevation at that point - and generates a full voxel data structure. This process requires generating a quadtree representation of the image, which is then processed into the octree structure. We used OpenCL to run kernels on the GPU for tracing per-pixel rays.
Data Structure:
The project involves primarily an octree data representation and a rendering pipeline that allows us to efficiently render (using per-pixel rays) and interact with a complex voxel game world. A voxel is essentially a pixel in the context of three-dimensional spatial representations. We divide space into a 3D grid, and each cube in the grid is either occupied or empty. A sparse octree allows us to represent a high detail voxel space while compressing spaces with similar data. This is especially useful in our case (a landscape), where there is lots of detail in a relatively tight span of vertical space, and very little detail below or above the surface. An octree allows us to save memory in those low detail areas by having larger leaf nodes that don’t need to hold information about their children.
Some examples of Voxel representations:
Minecraft: In Minecraft, each voxel is approximately one cubic meter.
Voxels are also frequently used to perform efficient 3D simulations.
The data structure used in this project is an octree, with each node represented by 11 unsigned integers. Octrees recursively divide space into 8 axis-aligned suboctants. Since octree nodes have 8 children, children are indexed with 3-bit values, where each bit represents the position of the child node along each axis.
Example of an octree node and the indexes of its child nodes.
The first two integers represent the status of each child node. The first 8 bits of the first integer represent whether or not the child node is ‘active’, (there are any active nodes in its tree). The first 8 bits of the second integer indicate whether the child is a leaf node. The next 8 integers are pointers (offsets in the overall octree buffer) to the child node. The last integer contains information about the color of the node. This representation makes operations more computationally efficient because each node has a consistent size - exactly 11 unsigned integers.
Rendering:
Rendering 3D environments in games traditionally involves using geometry with pre-defined vertices and faces, which is then sent to a library such a OpenGL to then be rendered in the right orientation and scale, along with lighting, occlusion and other effects. While this would be theoretically possible to do with our data structure, it would not take the most advantage of the data structure’s advantages, and would not be as much of an interesting comparison with a CPU implementation of rendering.
Instead, we opted for ray tracing, which involves firing ray from the camera for each pixel in the final render, and coloring that pixel according to what the ray strikes. This is an extremely parallelizable process, as each ray trace requires no communication with other rays, and there exists such a task for every single pixel in the render (in our case, 1920 x 1080 = 2073600 tasks). Additionally, an octree representation is perfect for ray tracing as the depth of the structure is O(log(N)) where N is the total number of voxels in the scene. Our particular octree representation also allows us to early-exit throughout the tracing process any time we come across a leaf node. Ray tracing also allows us to go further with lighting effects that use additional ray traces per-pixel and make the scene more visually interesting.
Additionally, ray tracing in this manner may benefit from SIMT execution on the GPU. Since the id of each thread is its coordinate in screen space, threads in the same block are going to be close to one another on-screen. This means they are likely to take mostly similar paths along the octree structure, which may allow some sharing of work within a block.
Heightmap:
In order to generate an interesting landscape that could show off the lighting effects of the simulation, it made sense to generate it from a heightmap. Many games use height maps to encode landscape information, since storing only the height at each point is a good way to store a convex surface. In our case we use a grayscale image which stores a scalar value at each 2D coordinate. This is simple and also makes it easy to verify visually whether the landscape is being generated correctly. Most heightmaps interpret the minimum value as minimum elevation, and vice versa. This would have created some pretty extreme terrain, ranging from the very bottom of the octree to the very top. We remapped the values in our heightmaps so the range was much tighter, which created more reasonable terrain which was more visually appealing and cheaper to interact with computationally.
Hardware:
This application was tested on a machine with both a GPU and CPU. The installed GPU was an NVIDIA RTX 3080 installed, with 12GB of VRAM. The system CPU was a stock 12700k, with 32GB of DDR4 memory installed.
Logistics:
Before the first frame is drawn, we load a high resolution height map from the file system, whose data is passed to a recursive function which constructs the quadtree data from the image. This quadtree data is then passed to a recursive function which builds out the octree.
We use a combination of OpenGL and OpenCL to render images in this project. For each frame, we deploy an OpenCL task, which writes its results to a texture. This texture then passed as the primary texture to an OpenGL shader, which renders a full screen quad to put the texture on screen. When deploying a task to the GPU, OpenCL allows us to easily define the block size as a parameter.
In order to collect data about performance, we measure time at various points throughout the process of building the data structure and rendering a frame each time we run the program. This allows us to see how tweaking high level variables such as the spatial resolution impacts every part of the application. We also automatically write the first frame to an image file.
Rendering Algorithm:
In order to render our voxel data structure, we designed a function which can run on our GPU which can trace a ray from an arbitrary point in space and give us information about the point in the octree that the ray hits. This algorithm is relatively straightforward, once it determines the ray’s entrypoint in the octree, it is simply a matter of marching through nodes either by pushing into a deeper node, popping into a higher node, or marching forward into a sibling node. The algorithm keeps track of a 3-bit index of the child position, and flips the correct bit for each operation. Additionally, we ‘rotate’ the entire coordinate system so that the ray is always moving in the positive X, Y ,and Z directions. For example, if the original ray direction is (-1, 1, 1), we will use a bitmask of 100 throughout the execution of the trace so that we can treat the system as though we are always moving in the positive directions through the coordinate system. This vastly reduced the number of cases we need to deal with when traversing across the octree. The code for this particular algorithm is inspired largely by this NVIDIA Paper, though our data structure differs significantly.
To render a single frame, we trace a ray out from the camera for each pixel on the screen. Once it strikes a node which is both a leaf node and active, or it leaves the octree entirely, we return. We return true or false based on whether we hit anything. If we hit, we also return the point in space that we hit, the color of the node we hit, as well as the normal of the surface. This allows us to perform lighting calculations which go beyond simply showing the base color at a point. Additionally, because this function is completely generic, we can not only use it to trace a ray out from the camera, but can also to compute direct and indirect lighting via path tracing. In our case we use a simplified version of monte carlo lighting collection, as well as a single ‘sun’ directional light. We can vary the number of indirect lighting samples to increase the quality and realism of the image, at the cost of performance.
Generating Octree From Heightmap:
The heightmap used.
The first step in generating the octree from our heightmap is building a quadtree in the heightmap which tells us the maximum and minimum height values at each subdivision of the heightmap. The quadtree adds nodes until it reaches the maximum resolution, then computes the maximum and minimum values, and passes those up to its parent nodes. In order to parallelize this process, we ran the top-level 4 recursive calls in parallel using OpenMP. There is no communication across calls, so this did not affect correctness.
After the quadtree, we progressively generated the octree, matching each node to the quadtree node it occupies in the heightmap. Using the quadtree information, from within a node we can easily make a decision as to whether the landscape lies entirely below, above, or inside the quadtree node. If the landscape is entirely above or below a node, it is a leaf node (below means an active node, above means an inactive node). If it is inside, it is an active non-leaf node. The maximum depth of the octree is a variable passed to this generation algorithm.
As much as it was desirable for the purposes of this project to do so, the octree generation was not sensibly parallelizable. Because child nodes used ‘pointer’ offset counts, the current size of the buffer needed to be kept track of throughout the algorithm. This value would need to be synchronized between independent threads at essentially all times, which would introduce significant overhead. Additionally, the individual buffers would need to be combined to be sent to the GPU.
In theory, it is possible to split the octree generation into 4 processes, each handling its own pair of top-level octants (combining the octants vertically). Each of these individual octrees could have their own offsets, and have their own independent buffers. These 4 buffers could be sent to the GPU individually and the trace algorithm on the GPU could be rewritten to use one of the four according to the first entrypoint of the ray. This likely would result in some speedup in the octree generation. Ultimately, however, the octree generation was actually a very small portion of the time spent before rendering the first frame, and we did not have enough time to dedicate to this experiment.
Updating the Octree in Real Time:
The most common way voxel games allow players to manipulate the environment is by placing and destroying individual blocks. In order to achieve this we wrote the same ray tracing algorithm we used on the GPU in C++, which allowed us to query the data structure on the GPU. We draw a ray out from the camera, and either enable or disable the hit block by simply flipping the correct bit. Once the data structure is updated, we can resend it to the GPU to update the render.
The max of depth of the octree, or the resolution of the landscape, is a variable which we can vary. We got the best (most visually appealing and impressive) results with a value of 11, which means the maximum number of non-leaf nodes in the tree is 8^10, or 1073741824. This would require 44 gigabytes of memory. This is well beyond the hardware limitations of both the main system (CPU + system RAM) and the GPU (VRAM) on the system we tested the application on. By keeping the terrain mostly flat we significantly increased the ratio of leaf to non leaf nodes, which brought the total size of the tree down to less than 40 megabytes.
The concept of each step of this process came together fairly early on, especially since we had a similar ray-tracing project to start from which gave us the infrastructure for OpenGL and OpenCL. The main iterative process in this project was resolving bugs in the tracing and lighting functions in the OpenCL kernel, which was very difficult to debug as it was running entirely on the GPU. Debugging largely involved writing specific colors to the screen in specific cases, which gave us information about how the algorithm was working.
The overall render time of the application was reduced significantly over the course of the project, primarily due to two problem areas:
Memory bandwidth. At first we were reloading and writing the render texture in OpenCL to the CPU each frame, which was extremely expensive. Removing this completely unnecessary step brought our frame time down by around 60%.
Taking advantage of thread blocks. For a large portion of the project, we were running the kernel with a configured block size of one. Increasing the block size to the optimal level (trial and error until render time was minimized) cut render time by an additional 66%.
Overall, the most difficult step of this project was getting each step working correctly in the first place. Afterwards, optimization primarily came down to distributing the work effectively across the threads.
The final results of the renders were surprisingly impressive. The GPU hardware we used was state of the art, but at the start of the project we expected render times at the least to be in the hundreds of milliseconds when doing indirect lighting sampling. In most cases, even at our max spatial resolution and with significant indirect lighting sampling, render times were well within what one would expect for a real-time game, sometimes even in the single digits of milliseconds. Of course, render times varied greatly depending on what was ‘on screen’, but we measured exclusively camera orientations and positions which kept the majority of the landscape on screen.
The results of parallelizing the pre-render steps (specifically octree generation) were much more disappointing. Admittedly optimizing these steps was not the primary goal of this project, and since they were recursive functions initial expectations for speedup across threads were not high. Our primary parallelization for the quad tree - adding an OpenMP “parallel for” statement above the top-level set of recursive calls - actually resulted in below 1 speedup.
All times in the below charts are in microseconds.
The most significant single optimization of render time came with optimizing the thread block size.
For constant resolution and block size, indirect samples had by far had the strongest impact on render time.
For us the most interesting variable to tweak was spatial resolution, which had an impact on all steps in the process.
Step time distribution:
By far the most expensive part of the pre-render process is the quadtree generation. Frequently the quadtree generation was almost 20 times the cost of the octree generation. I suspect this is because we allocated new objects at each step, rather than just populating a buffer.
If there was more time to work on this project I would certainly attempt to generate the octree in a buffer in a similar method to the way the quadtree was generated, which would probably drastically reduce pre render time.
At a spatial resolution of 11:
Average Quadtree Construction Time: 1703592 microseconds (1.7 seconds)
Average Octree Construction Time: 97084 microseconds (97 milliseconds)
Performance Limitations:
The element of this problem which most limited our performance during rendering was most likely memory bandwidth on the GPU threads. Because of the pointer system used in the octree, threads were often jumping around across the data structure, which was probably not optimal for cache hit rate. Since all of the gpu operations on the octree were read-only, it is unlikely that memory coherence played a significant role in the render performance. Overall, we believe we got fairly close to the compute limitations in the rendering process. The best way to increase performance going forward would most likely be to simply do less computation, for example: storing lighting information on the octree so that it does not need to be recomputed every frame.
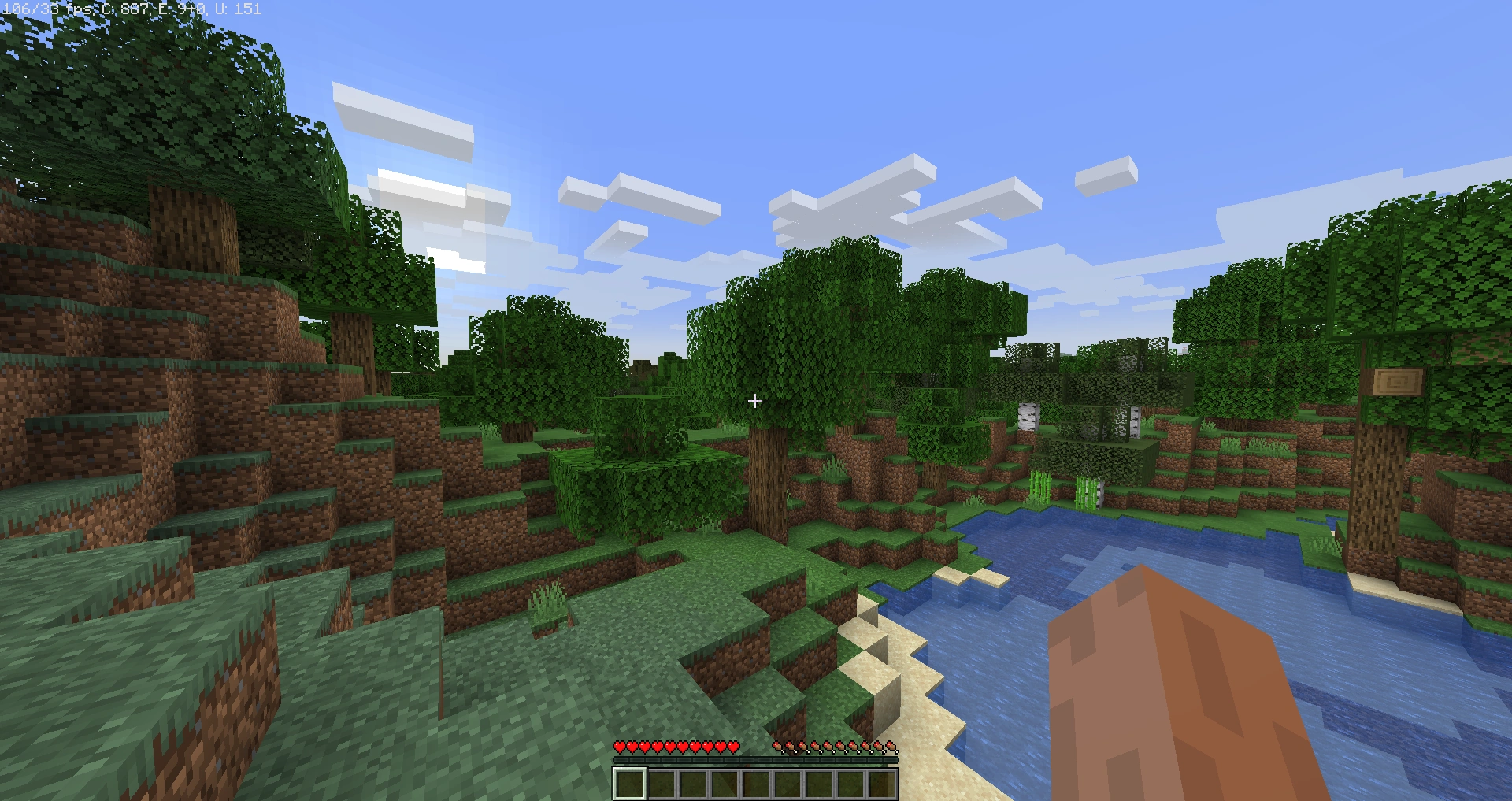
Render Screenshots:
Final render configuration at a spatial resolution of 11
Final render configuration at a spatial resolution of 4
Final render settings with harsher (more realistic) lighting.
Final render settings with softer (more game-like) lighting.
Color settings used during debug.
Smaller scale, demonstrating noise caused by monte carlo indirect lighting.
Full scale, single color, no indirect lighting.
Work Distribution:
This project was done by one person, so this is not applicable.